Podstawowa Konfiguracja Routera Tp-Link
23 czerwca, 2022Tematem dzisiejszego wpisu jest konfiguracja routera domowego TPLINK C6U. Wszystkie opisane operacje będzie można powtórzyć na sporej części innych routerów...
Czytaj dalej

System szesnastkowy, czyli inaczej heksadecymalny to system zawierający cyfry od 0 do 9 oraz litery od A do F (odpowiadające liczbom od 10 do 15). System szesnastkowy jest używany między innymi do tworzenia unikalnych adresów MAC (adres fizyczny karty sieciowej) oraz do adresowania za pomocą protokołu internetowego wersji 6. Jest doskonały do tworzenia unikatowych oraz zajmujących stosunkowo mało miejsca na zapis liczb.
Chociażby zapis informacji o kolorze gdzie dla porównania zapis kolor szarego to 100 100 100 w systemie dziesiętnym, natomiast 40 40 40 w systemie szesnastkowym – zajmuje dwie pozycje na zapis jednego koloru zamiast trzech (maksymalne wartości dla koloru to FF w szesnastkowym). Przyjmuje się, aby liczby zaczynające się literą z lewej strony poprzedzać 0, czyli zamiast AH zapisać 0AH – jednak nie jest to konieczne.
Aby dokonać konwersję z liczb dziesiętnych na szesnastkowe, możemy skorzystać z dwóch sposobów. Pierwszy z nich to konwersja na system binarny, podział na sekcje zawierający po 4 bity a następnie obliczenie wartości szesnastkowej danych 4 bitów. Poniżej tabela zamiany 4 bitowych liczb binarnych na szesnastkowe.
Za przykład dajmy sobie liczbę 239D.
1) Zamieniamy na binarny:
239D = 11101111B
2) Dzielimy na sekcje zawierający:
1110 | 1111
3) Zmieniamy sekcję:
E | F
4) Gotowe!:
0EFH
Jednak szybszym sposobem zamiany liczb dziesiętnych na szesnastkowe jest dokonania dzielenia podobnego do dzielenia które wykonywaliśmy wcześniej w systemie binarnym.
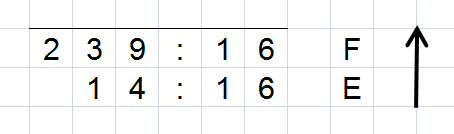
0EFH to reszta z dzielenia liczb 239 oraz 14 przez 16.
Konwersję szesnastkowego na dziesiętny przeprowadzamy w sposób podobny do pierwszego opisanego: zamieniamy z szesnastkowego na binarny i dokonujemy zamiany z binarnego na dziesiętny. Przedstawiono poniżej po lewej stronie.
0EFH = 1110 | 1111D = 239D
0EFH = 15 * 161 + 16 * 160 = 239D
Możemy również pomnożyć rzędy danej liczby przez kolejne potęgi szesnastu i zsumować je ze sobą – co jednak będzie bardziej skomplikowane. Proces przedstawiony po prawej stronie powyżej.
Również w systemie szesnastkowym, jak w każdym systemie liczbowym występują działania na liczbach. Jednak działania na liczbach szesnastkowych nie są zbyt często wykorzystywane. Głównie podstawowe działania (dodawanie i odejmowanie) mogą być podczas obliczania koloru podczas projektowania kolorystyki strony. Dlatego mogę zaproponować konwersję na liczby binarne, dokonanie działań na binarnych i powrót z binarnych do szesnastkowych. Dalej jednak postaram się omówić operacje na liczbach szesnastkowych, pomijając szczegółowe opisanie wcześniej zaproponowanego sposobu.
Dokonujemy je zwykle za pomocą działania pisemnego. W poniższym przykładzie dodamy liczbę 0E do 0AF. System przesunięcia nadmiaru działa podobnie jak w systemie binarnym dając 1 tego systemu liczbowego. Przedstawiłem tutaj po lewej dodawanie w systemie szesnastkowym, po prawej w systemie binarnym.
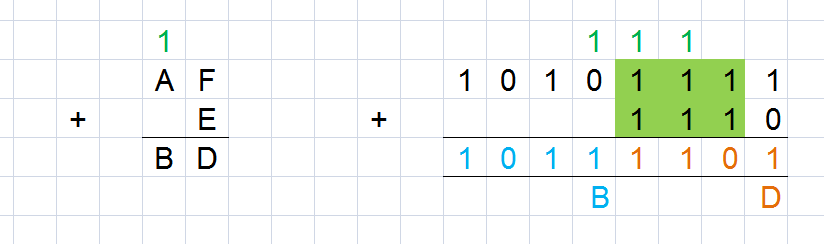
Przy tym należy pamiętać że system nadmiaru działa tylko wtedy, kiedy suma poszczególnych cyfr przekracza cyfrę F.
Odejmujemy również za pomocą działania pisemnego. W poniższym przykładzie odejmiemy 4FH od 0F45H. Również tutaj pożyczka działa podobnie jak w systemie binarnym. Przedstawiłem tutaj po lewej odejmowanie w systemie szesnastkowym, po prawej w systemie binarnym.
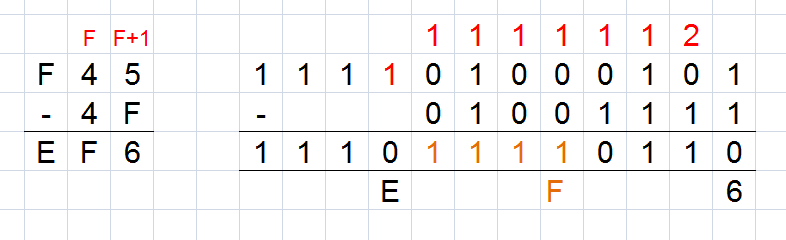
Mnożenie jest bardziej skomplikowaną sprawą niż wcześniej przedstawione działania i wymaga pewnego przyzwyczajenia oraz oderwania się od tradycyjnego, dziesiętnego modelu mnożenia. Oczywiście schemat sam w sobie jest podobny do mnożenia pisemnego dziesiętnego, jednak występowanie 16 cyfr (zamiast 10) wymaga zastosowania pewnego systemu.

W tym systemie:
W poniższym przykładzie pomnożymy liczbę 0F44H przez 0D5H. Wynikiem mnożeniem będzie liczba 832404D. Po lewej stronie jest przedstawione działanie w formie pisemnej, natomiast po prawej poszczególne wyniki mnożenia liczb dziesiętnych i zamiany ich na szesnastkowe. W tym wypadku pozwoliłem sobie od razu dodać do siebie pokazać wynik mnożenia liczby 0F44H przez cyfry mnożnika 0D5H.

Dzielenie w systemie szesnastkowym jest również podobne do dzielenia w systemie pisemnym dziesiętnym. W poniższym przykładzie dzielimy liczbę 223D przez 5D. Wynikiem dzielenia jest liczba 44D z resztą 3D. Należy pamiętać o tym, by zmieniać liczby heksadecymalne na dziesiętne podczas dzielenia, by ustrzec się błędów wynikających z braku konwersji.
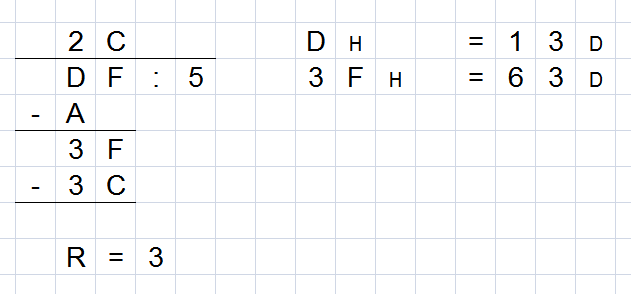
.
Tematem dzisiejszego wpisu jest konfiguracja routera domowego TPLINK C6U. Wszystkie opisane operacje będzie można powtórzyć na sporej części innych routerów...
Czytaj dalejKażdy z nas wie, że komputer do poprawnego działania musi przechowywać w sobie odpowiednią ilość informacji. Wszyscy też zauważyli, że...
Czytaj dalejGdy przeglądamy dostępne modele procesorów, widzimy mnogość cyfr. Czasami spotkamy się także z jakimś oznaczeniem literowym. Co one właściwie oznaczają?...
Czytaj dalej